TUTORIALS ESP32 The objective of this esp32 tutorial is to explain how to apply the SHA1 hashing algorithm to a text input using Espruino, running on the ESP32. The tests were performed using a DFRobot’s ESP32 module device integrated in a ESP32 development board.
ESP32 Espruino Tutorial: Applying the SHA1 hash algorithm
DFRobot
Apr 23 2018 261598
The objective of this esp32 tutorial is to explain how to apply the SHA1 hashing algorithm to a text input using Espruino, running on the ESP32. The tests were performed using a DFRobot’s ESP32 module device integrated in a ESP32 development board.
Introduction
The objective of this post is to explain how to apply the SHA1 hashing algorithm to a text input using Espruino, running on the ESP32. You can read more about SHA1 here.
The tests were performed using a DFRobot’s ESP32 module device integrated in a ESP32 development board.
The codeFirst of all, we will need to include the crypto module, in order to access the SHA1 hashing functionality.
crypto = require('crypto');
Now that we have access to the module functionality, we simply call the SHA1 function, which receives as input the value to which the hashing should be applied and returns as output an ArrayBuffer of 20 bytes with the result [1].
This is the value expected since the algorithm generates a 160 bits result, which corresponds to 20 bytes [2].
We will call this function to hash a string with a content equal to “message” and store the result in a variable.
var shaArray =crypto.SHA1("message");
In order to confirm that our result is correct, we will convert it to a hexadecimal string and compare it with the result from applying the SHA1 algorithm to the same input from an online tool.
To do it, we will simply iterate the whole array, convert each element from byte to hexadecimal string and append it to a final string variable. So, we first declare an iterator variable and an empty string, to hold the final hexadecimal string.
Then, we will iterate the array from zero to the size of the array minus 1 (arrays are zero based in JavaScript). We can get the length of the array from its length property.
To convert a number to a string we simply call the toString method. Nonetheless, in our case, we want it to be converted to a different format, and thus we can pass as input of the toString method the base to use for representing the resulting number as string [3]. The function accepts a value for the base from 2 to 36 [3].
You can check below the procedure needed for performing the mentioned conversion from the array to the hexadecimal string.
var i = 0; var finalString = ""; for (i = 0; i< shaArray.length; i++){ finalString = finalString + shaArray[i].toString(16); }
Finally we will declare a variable containing the hexadecimal string resulting from using the previously mentioned online tool to hash the same “message” content. Next we will print our result and then print the comparison between our result and the one from the online tool. They should be equal.
You can check the full source code below.
crypto = require('crypto'); var shaArray =crypto.SHA1("message"); var i = 0; var finalString = ""; for (i = 0; i< shaArray.length; i++){ finalString = finalString + shaArray[i].toString(16); } var shaOnlineString = "6f9b9af3cd6e8b8a73c2cdced37fe9f59226e27d"; console.log(finalString); console.log(finalString == shaOnlineString);
Testing the code
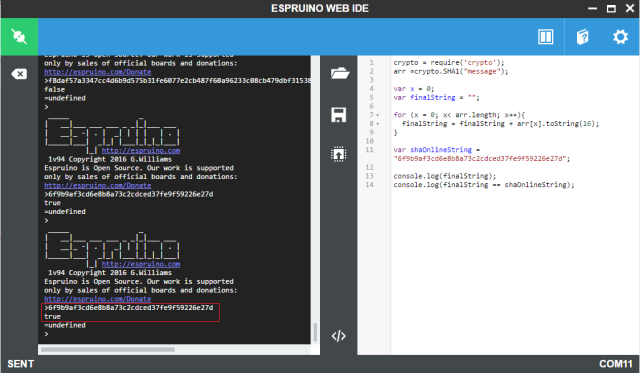
To test the code, simply upload it and run it using the Espruino web IDE. You should get an output similar to figure 1. As can be seen, the final hexadecimal string is printed and the result of the comparison is true, indicating that the result we obtained is correct.